题目内容
当A+B+C=2013时(A、B、C是非零自然数)试求A×B×C的最大值与最小值?(最大值可以写成算式,但最小值要求写出具体值)
分析:要使三个数的积最大,A、B、C应相差最小,2013÷3=671;所以A、B、C应为671,然后求三个数的积即可;
要使三个数的积最小,A、B、C应相差最大,因为A、B、C是非零的自然数;所以A、B、C应为1、1、2011,然后求三个数的积即可.
要使三个数的积最小,A、B、C应相差最大,因为A、B、C是非零的自然数;所以A、B、C应为1、1、2011,然后求三个数的积即可.
解答:解:要使三个数的积最大,A、B、C应相差最小,2013÷3=671;
所以A、B、C应为671,
671×671×671=302111711;
要使三个数的积最小,A、B、C应相差最大,因为A、B、C是非零的自然数;
所以A、B、C应为1、1、2011,
1×1×2011=2011.
答:A×B×C的最大值的算式是671×671×671;最小值是2011.
所以A、B、C应为671,
671×671×671=302111711;
要使三个数的积最小,A、B、C应相差最大,因为A、B、C是非零的自然数;
所以A、B、C应为1、1、2011,
1×1×2011=2011.
答:A×B×C的最大值的算式是671×671×671;最小值是2011.
点评:本题考查了数字问题,要记住规律:当两个数差越小积越大,当两个数差越大积越小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
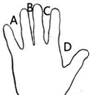 如图为手的示意图,在各个手指间标记字母A,B,C,D,请按照图中箭头所示方向从A开始连续的正整数1、2、3、4、5、6、…,A→B→C→D→C→B→A→B→C→…当字母C第201次出现时,恰好数到的数是
如图为手的示意图,在各个手指间标记字母A,B,C,D,请按照图中箭头所示方向从A开始连续的正整数1、2、3、4、5、6、…,A→B→C→D→C→B→A→B→C→…当字母C第201次出现时,恰好数到的数是