题目内容
下列说法错误的是
- A.直径为2厘米的圆,它的面积是π平方厘米
- B.一段弧长是4π,圆心角是60°,则所在圆的半径是12
- C.一个圆环的外直径是6,内直径是2,那么这个圆环的面积是32π
- D.当圆心角扩大2倍,半径也扩大2倍,则弧长扩大到原来的4倍.
C
分析:根据圆的面积公式S=πr2判断A的正误;根据弧长公式L=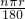 判断B与D的正误;根据圆环的面积公式S=π(R2-r2)判断C的正误.
判断B与D的正误;根据圆环的面积公式S=π(R2-r2)判断C的正误.
解答:A、π(2÷2)2=π,所以判断正确;
B、因为L=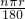 ,所以r=180L÷(nπ),
,所以r=180L÷(nπ),
即180×4π÷(60π)=12,
所以判断正确;
C、π(6÷2)2-π(2÷2)2,
=9π-π,
=8π;
所以判断错误;
D、因为L=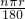 ,
,
所以L′=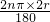 =4×
=4×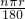 =4L,
=4L,
所以判断正确;
故选:C.
点评:本题主要是灵活利用面积公式S=πr2和弧长公式L=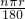 解决问题.
解决问题.
分析:根据圆的面积公式S=πr2判断A的正误;根据弧长公式L=
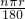 判断B与D的正误;根据圆环的面积公式S=π(R2-r2)判断C的正误.
判断B与D的正误;根据圆环的面积公式S=π(R2-r2)判断C的正误.解答:A、π(2÷2)2=π,所以判断正确;
B、因为L=
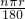 ,所以r=180L÷(nπ),
,所以r=180L÷(nπ),即180×4π÷(60π)=12,
所以判断正确;
C、π(6÷2)2-π(2÷2)2,
=9π-π,
=8π;
所以判断错误;
D、因为L=
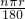 ,
,所以L′=
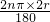 =4×
=4×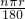 =4L,
=4L,所以判断正确;
故选:C.
点评:本题主要是灵活利用面积公式S=πr2和弧长公式L=
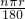 解决问题.
解决问题. 
练习册系列答案
相关题目