题目内容
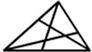 数一数,如图中有( )个三角形.
数一数,如图中有( )个三角形.分析:不在同一直线上三点可以确定一个三角形,据此即可判断.从6条直线中选3条,第一条有6种选法,第二条有5种选法,第三条有4种选法,共有6×5×4种选法.但是每一种被重复计算了6次,所以不同的选法应为
6×5×4=20种.
| 1 |
| 6 |
解答:解:(1)图中有6条直线.一般来说,每3条直线能围成一个三角形,但是这3条直线如果相交于同一点,那么,它们就不能围成三角形了.
从6条直线中选3条,有
×6×5×4=20种选法(见说明),
每次选出的3条直线围成一个三角形,但是在图中,每个顶点处有3条直线通过,它们不能围成三角形,因此,共有20-3=17个三角形.
故选:A.
从6条直线中选3条,有
| 1 |
| 6 |
每次选出的3条直线围成一个三角形,但是在图中,每个顶点处有3条直线通过,它们不能围成三角形,因此,共有20-3=17个三角形.
故选:A.
点评:本题主要考查了三角形的认识,按正确的顺序计算三角形的个数是解决本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 数一数,如图中有( )条线段.
数一数,如图中有( )条线段.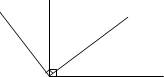 数一数,如图中有( )个角.
数一数,如图中有( )个角.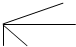 数一数,如图中有( )个角.
数一数,如图中有( )个角.
