题目内容
计算下面各角的度数.
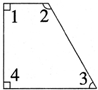
(1)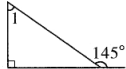 ∠1=
∠1=
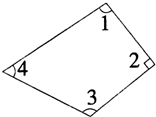
(2)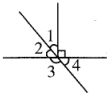 ∠1=40°那么∠2=
∠1=40°那么∠2=
(3)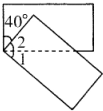 ∠1=
∠1=
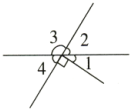
(4)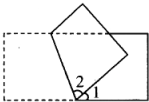 ∠1=40°,∠2=
∠1=40°,∠2=
(1)
 ∠1=
∠1=55°
55°
;(2)
 ∠1=40°那么∠2=
∠1=40°那么∠2=50°
50°
,∠3=130°
130°
,∠4=50°
=50°
;(3)
 ∠1=
∠1=40°
40°
,∠2=50°
50°
;(4)
 ∠1=40°,∠2=
∠1=40°,∠2=70°
70°
.分析:(1)先根据平角的定义,用180°减去145°求出三角形中另一个锐角的度数,再利用三角形的内角和是180°,用180°减去三角形另外两个内角的度数即可;
(2)根据直角的定义,用90°减去∠1即得∠2的度数,再根据平角的定义,用180°减去∠2即得∠3的度数,再用180°减去∠3即得∠4的度数;
(3)根据直角的定义,用90°减去40°即得∠2的度数,再用90°减去∠2的度数即得∠1的度数;
(4)根据平角的定义以及折叠前后的角相等,用180°减去∠1的度数再除以2即得∠2的度数.
(2)根据直角的定义,用90°减去∠1即得∠2的度数,再根据平角的定义,用180°减去∠2即得∠3的度数,再用180°减去∠3即得∠4的度数;
(3)根据直角的定义,用90°减去40°即得∠2的度数,再用90°减去∠2的度数即得∠1的度数;
(4)根据平角的定义以及折叠前后的角相等,用180°减去∠1的度数再除以2即得∠2的度数.
解答:解:(1)180°-145°=35°,
∠1=180°-90°-35°=55°;
(2)∠2=90°-∠1=90°-40°=50°,
∠3=180°-∠2=180°-50°=130°,
∠4=180°-∠3=180°-130°=50°;
(3)∠2=90°-40°=50°,
∠1=90°-∠2=90°-50°=40°;
(4)∠2=(180°-40°)÷2
=140°÷2
=70°.
故答案为:(1)55°;(2)50°,130°,50°;(3)40°,50°;(4)70°.
∠1=180°-90°-35°=55°;
(2)∠2=90°-∠1=90°-40°=50°,
∠3=180°-∠2=180°-50°=130°,
∠4=180°-∠3=180°-130°=50°;
(3)∠2=90°-40°=50°,
∠1=90°-∠2=90°-50°=40°;
(4)∠2=(180°-40°)÷2
=140°÷2
=70°.
故答案为:(1)55°;(2)50°,130°,50°;(3)40°,50°;(4)70°.
点评:本题考查求角的度数,主要是应用三角形内角和是180度以及平角与直角的定义解决问题.

练习册系列答案
相关题目
 计算下面各角的度数.
计算下面各角的度数.