题目内容
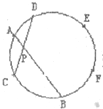 一个圆上有6个点(如图),两两连线时,在圆内最多可以有
一个圆上有6个点(如图),两两连线时,在圆内最多可以有30
30
个交点.分析:根据图形和线段的定义,将图形中的点两两相连,即可解决问题.
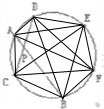

解答:解:任意圆内接四边形在圆内最多有两个交点即对角线的交点,则这6个点可以构造出
=
=15个圆内接四边形,每一个圆内接四边形有2个交点,则本题最多可以有30个交点.
故答案为:30.
| C | 4 6 |
| C | 2 6 |
故答案为:30.
点评:解答此题的关键是连接圆上的每四个顶点构成一个内接四边形,由此即可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
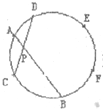 一个圆上有6个点(如图),两两连线时,在圆内最多可以有________个交点.
一个圆上有6个点(如图),两两连线时,在圆内最多可以有________个交点.