题目内容
8.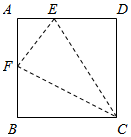 如图把长方形纸ABCD的一角折起,使点D恰好与AB的中点F重合,若三角形AEF的面积是3,三角形FBC的面积是7,三角形EFC的面积是多少?
如图把长方形纸ABCD的一角折起,使点D恰好与AB的中点F重合,若三角形AEF的面积是3,三角形FBC的面积是7,三角形EFC的面积是多少?
分析 由S△FBC=$\frac{1}{2}$BC×FB,又因为点F恰好是AB边的中点,因为S△FBC=7,所以$\frac{1}{4}$AB×BC=7,即AB×BC=28;又由长方形ABCD的面积=AB×BC,从而得出长方形的面积;又因为S△EFC=S△DEC,用长方形的面积减去△FBC和△AEF的面积除以2就是三角形EFC的面积.据此解答.
解答 解:因为点F恰好是AB边的中点,所以FB=$\frac{1}{2}$AB,
又因为S△FBC=$\frac{1}{2}$BC×FB,因为点F恰好是AB边的中点,
所以S△FBC=$\frac{1}{2}$×$\frac{1}{2}$AB×BC=$\frac{1}{4}$AB×BC,
又因为S△FBC=7,
所以$\frac{1}{4}$AB×BC=7,
所以AB×BC=28,
又因为长方形ABCD的面积=AB×BC,
所以S长方形ABCD=28平方厘米,
又因为△EFC和△DEC对称,所以又因为S△EFC=S△DEC,
三角形EFC的面积为:
(28-3-7)÷2
=18÷2
=9.
答:三角形EFC的面积是9.
点评 此题主要是根据条件找△FBC的边与长方形ABCD的边之间的关系.

练习册系列答案
相关题目
16.直接写出得数
| 3.14×0.2= | 3.14×50= | $\frac{3}{4}$:16= | 12:$\frac{3}{5}$= |
| 0.3×$\frac{5}{6}$= | $\frac{3}{5}$:$\frac{9}{10}$= | 1÷$\frac{7}{8}$= | 4:20%= |
| $\frac{3}{5}$÷$\frac{7}{45}$= | $\frac{2}{9}$×12= |