题目内容
18.甲、乙、丙三人同时到理发店理发,只有一位理发师当班.已知甲理发要10分钟,乙理发要20分钟,丙理发要15分钟.按照( )的顺序,才能使他们等候的时间的总和最少.| A. | 甲→乙→丙 | B. | 乙→丙→甲 | C. | 甲→丙→乙 | D. | 丙→甲→乙 |
分析 三个人同时来到理发店理发,有1个人理发其他两个人就要等着,由此可以看出自然是花时间少的人先理发,等候时间的总和就会越少.即按甲→丙→乙的顺序就能使等侯的时间和最少;据此解答.
解答 解:三人理发的顺序依次是:甲→丙→乙,
10×3+15×2+20×1
=30+30+20
=80(分钟)
答:他们三人理发的顺序依次是:甲→丙→乙,等候时间的总和最少是80分钟.
故选:C.
点评 本题实际是统筹优化问题,因为等候的总时间与等候的人数和每个人需要的时间有关,在人数不变的情况下,需要让用时最少的先理发.

练习册系列答案
相关题目
6.用竖式计算.
| 32×15= | 25×18= | 46×36= |
| 28×56= | 70×79= | 43×60= |
3.下面三个数中,既不是质数又不是合数的是( )
| A. | 1 | B. | 2 | C. | 0 |
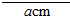 如图线段的长为acm.
如图线段的长为acm.