题目内容
【题目】如图所示，P为长方形ABCD的对角线BD上任意一点，M为线段PC的中点，如果△APB的面积是
，则△BCM的面积是多少？
【答案】
【解析】
根据BD是长方形ABCD的对角线，可知△APB和△APD的面积之和是长方形ABCD面积的一半，又因为△APD和△BPC等底，它们的高的和等于AB，所以△APD和△BPC的面积之和也等于长方形面积的一半，所以△APB和△BPC的面积相等，根据M为线段PC的中点，可知△BCM的面积是△BPC面积的一半，据此得解。
设长方形ABCD的面积是S，
∵BD是长方形ABCD的对角线
∴S△APB＋S△APD＝
S
又∵S△BPC＋S△APD＝S
∴S△BPC＝S△APB＝
∵M为线段PC的中点
∴S△BCM＝S△BPC＝
答：△BCM的面积是。
练习册系列答案
相关题目
【题目】水是生命之源，学校对同学们进行了节约用水教育。笑笑测试了一个打开水龙头的出水量，并记录了下表的数据。
时间/秒 | 0 | 10 | 20 | 30 | 40 | 50 | … |
出水量/L | 0 | 3 | 6 | 9 | … |
（1）把上表填写完整。
（2）时间与出水量成正比吗？解释原因。
（3）先根据上表描点，再顺次连接各点，你发现了什么？
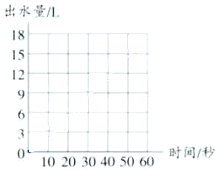
（4）点（60，18 ）在所连的直线上吗？这一点表示什么含义？
