题目内容
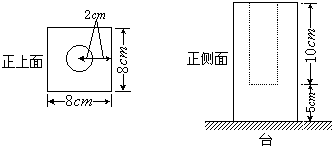
如图是从一个立体图形的正上面与正侧面看到的图形,试回答下列问题:
(1)以每秒1毫升的速度,往容器内注水时,水面到离台面10cm的地方为止,需要多少秒?
(2)求这个立体图形的体积.
(3)求这个立体图形的表面积.(π=3)
(1)以每秒1毫升的速度,往容器内注水时,水面到离台面10cm的地方为止,需要多少秒?
(2)求这个立体图形的体积.
(3)求这个立体图形的表面积.(π=3)

分析:(1)这个容器里面是一个圆柱形,圆柱的底面半径是2cm,水面离台面10厘米,水的高度是5厘米,根据圆柱体的体积公式计算出容积,再除以速度即可.
(2)用正方体的体积减去圆柱体的体积即可.
(3)表面积等于正方体的体积加上圆柱的侧面积.
(2)用正方体的体积减去圆柱体的体积即可.
(3)表面积等于正方体的体积加上圆柱的侧面积.
解答:解:(1)2×2×3×(10-5)
=12×5
=60cm3,
60÷1=60(秒).
答:需要60秒.
(2)8×8×(10+5)-2×2×3×10
=960-120
=840cm3.
答:体积是840cm3.
(3)底面积8×8×2=128cm2;
外侧面的面积为8×(10+5)×4=480cm2;
内侧面积为4×3×10=120cm2;
表面积为128+480+120
=728cm2.
答:表面积是728cm2.
=12×5
=60cm3,
60÷1=60(秒).
答:需要60秒.
(2)8×8×(10+5)-2×2×3×10
=960-120
=840cm3.
答:体积是840cm3.
(3)底面积8×8×2=128cm2;
外侧面的面积为8×(10+5)×4=480cm2;
内侧面积为4×3×10=120cm2;
表面积为128+480+120
=728cm2.
答:表面积是728cm2.
点评:此题主要考查长方体与圆柱的表面积及体积的计算,解答关键是理解长方体与圆柱的特征.

练习册系列答案
相关题目
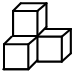 (2004?丹阳市)如图是由4个完全相同的小正方体堆成的一个立体图形,从上面看这个图形,可以看到这个立体图形的( )个面.
(2004?丹阳市)如图是由4个完全相同的小正方体堆成的一个立体图形,从上面看这个图形,可以看到这个立体图形的( )个面. 一个用小正方体搭成的立体图形,从前面看到的是图形①(如图),从上面看到的是图形②(如图),那么搭成这样一个立体图形最少要( )个小正方体.
一个用小正方体搭成的立体图形,从前面看到的是图形①(如图),从上面看到的是图形②(如图),那么搭成这样一个立体图形最少要( )个小正方体.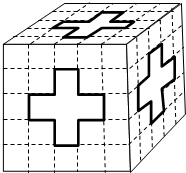 有一个棱长5厘米的正方体木块,从它的每个面都有一个穿透的完全相同的孔(如图),这个立体图形的体积是
有一个棱长5厘米的正方体木块,从它的每个面都有一个穿透的完全相同的孔(如图),这个立体图形的体积是 由4个大小相同的小正方体搭成一个立体图形,从左面看到的形状如图,则这个立体图形的搭法不可能是( )
由4个大小相同的小正方体搭成一个立体图形,从左面看到的形状如图,则这个立体图形的搭法不可能是( )