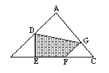
题目内容
【题目】如图,在△ABC中,AD=![]() AB,BE=EF=FC,CG=
AB,BE=EF=FC,CG=![]() GA,求阴影部分面积占三角形ABC面积的几分之几?
GA,求阴影部分面积占三角形ABC面积的几分之几?
【答案】![]() .
.
【解析】
试题分析:因为CG=![]() GA,所以AG=
GA,所以AG=![]() AC,可以先求出边上的3个小三角形与S△ABC的面积之间的关系:S△ADG=
AC,可以先求出边上的3个小三角形与S△ABC的面积之间的关系:S△ADG=![]() ×
×![]() ×S△ABC=
×S△ABC=![]() S△ABC,S△BDE=
S△ABC,S△BDE=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,S△CFD=
S△ABC,S△CFD=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,然后求出这三个三角形的和与△ABC的关系,进而求出阴影部分面积占三角形ABC面积的几分之几.
S△ABC,然后求出这三个三角形的和与△ABC的关系,进而求出阴影部分面积占三角形ABC面积的几分之几.
解:S△ADG=![]() ×
×![]() ×S△ABC=
×S△ABC=![]() S△ABC,
S△ABC,
S△BDE=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
S△CFD=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
所以S△ADG+S△BDE+S△CFD,
=(![]() +
+![]() +
+![]() )S△ABC,
)S△ABC,
=![]() S△ABC,
S△ABC,
所以S阴影=(1﹣![]() )SABC=
)SABC=![]() S△ABC;
S△ABC;
答:阴影部分的面积占三角形△ABC面积的![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目