题目内容
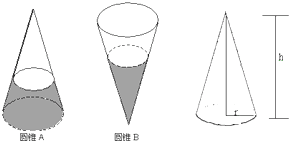
【题目】如图，A和B为二个全等的圆锥容器，今将水分别倒入圆锥A和圆锥B中，使得这二个圆锥容器内的水位高度都正好是圆锥的高的一半，试求在圆锥A中水的容量和在圆锥B中水的容量的比．
（圆锥的体积=π r2h，其中r为底圆的半径，h为圆锥的高）
【答案】1：7．
【解析】
试题分析：此题可以通过圆锥的体积公式求出水的体积，然后再用甲容器内水的体积除以乙容器内水的体积即可．再求水的体积和整个圆锥容器的容积时，可以设出半径和高度，那么圆锥容器的半径和高度分别是水的2倍，然后利用圆锥的体积公式解答．
解：设圆锥的底面半径为2r，高为2h，
A圆锥内水的体积为：
π（2r）2×2h﹣πr2h=
πr2h，
B圆锥内水的体积为：πr2h，
A容器内水的体积是B容器内水的体积的：πr2h÷πr2h=7，
所以，A容器中水的体积是B容器中水的体积的7倍．
答：圆锥A中水的容量和在圆锥B中水的容量的比是1：7．
练习册系列答案
相关题目
