Question

一个等腰梯形的上底是下底的两倍，请在这个梯形中表示出四分之一．

Answer 1

分析：先做EF∥BC，但要保证：AG+

1

2

DF=FC，过AE的中点做垂线，再做AB的垂线，使BM=FN，所以过G、E、M点的直线就是梯形面积的四等分的直线．

解答：解：先做EF∥BC，但要保证：AG+

1

2

DF=FC，过AE的中点做垂线，再做AB的垂线，使BM=FN，所以过G、E、M点的直线就是梯形面积的四等分的直线．
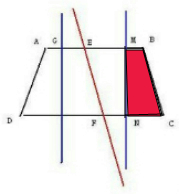
如图涂色的部分就是这个梯形面积的四分之一．

点评：本题作图的关键是确定EF的位置，即AE+DF=ED+FC．