题目内容
三角型ABC是一个等腰直角三角型,其中角C=90°,直角边的长度是1,现在以C为圆心,把三角形ABC顺时针旋转90°,那么AB边在旋转时所扫过的面积是________(保留两位小数,圆周率取3.14).
0.68
分析:过C作CE⊥AB,根据等腰直角三角形的性质和旋转的性质得到以点C为圆心,把三角形ABC顺时针旋转90度得到△DAC,两个三角形组成一个等腰直角三角形ABD;由于A与B离C点最远,点E离C点最近,则AB边在旋转时所扫过的面积为弧EF、BE、弧BAD、FD所围成的图形面积,然后根据圆的面积公式、三角形的面积公式以及扇形的面积公式计算即可.
解答:如图,过C作CE⊥AB △ABC绕点C顺时针旋转90度得到△DAC,CF为CE的对应线段,
△ABC绕点C顺时针旋转90度得到△DAC,CF为CE的对应线段,
因为△ABC是一个腰为1的等腰直角三角形,
所以AB= AB=
AB= ,
,
所以CE= AB=
AB= ,
,
因为AB边在旋转时所扫过的面积为弧EF、BE、弧BAD、FD所围成的图形面积,
所以AB边在旋转时所扫过的面积=半圆BD的面积-△CBE的面积-△CFD的面积-扇形CEF的面积
= π?12-2?
π?12-2? ?
? ?
? -
-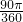

= π-
π- ,
,
= ×3.14-
×3.14- ,
,
=1.775-0.5,
=0.6775,
≈0.68.
答:AB边在旋转时所扫过的面积是0.68.
故答案为:0.68.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应相等相等,对应角相等;对应点与旋转中心的连线段的夹角等于旋转角.也等腰直角三角形的性质以及扇形的面积公式.
分析:过C作CE⊥AB,根据等腰直角三角形的性质和旋转的性质得到以点C为圆心,把三角形ABC顺时针旋转90度得到△DAC,两个三角形组成一个等腰直角三角形ABD;由于A与B离C点最远,点E离C点最近,则AB边在旋转时所扫过的面积为弧EF、BE、弧BAD、FD所围成的图形面积,然后根据圆的面积公式、三角形的面积公式以及扇形的面积公式计算即可.
解答:如图,过C作CE⊥AB
 △ABC绕点C顺时针旋转90度得到△DAC,CF为CE的对应线段,
△ABC绕点C顺时针旋转90度得到△DAC,CF为CE的对应线段,因为△ABC是一个腰为1的等腰直角三角形,
所以AB=
 AB=
AB= ,
,所以CE=
 AB=
AB= ,
,因为AB边在旋转时所扫过的面积为弧EF、BE、弧BAD、FD所围成的图形面积,
所以AB边在旋转时所扫过的面积=半圆BD的面积-△CBE的面积-△CFD的面积-扇形CEF的面积
=
 π?12-2?
π?12-2? ?
? ?
? -
-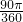

=
 π-
π- ,
,=
 ×3.14-
×3.14- ,
,=1.775-0.5,
=0.6775,
≈0.68.
答:AB边在旋转时所扫过的面积是0.68.
故答案为:0.68.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应相等相等,对应角相等;对应点与旋转中心的连线段的夹角等于旋转角.也等腰直角三角形的性质以及扇形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 块.________.
块.________.