题目内容
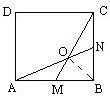 在图中ABCD是边长为9厘米的正方形正M、N分别为AB边与BC边的中点,AN与CM相交于点O,求四边形AOCD的面积是多少?
在图中ABCD是边长为9厘米的正方形正M、N分别为AB边与BC边的中点,AN与CM相交于点O,求四边形AOCD的面积是多少?分析:如图,因为M、N分别为AB边与BC边的中点,根据三角形和正方形的面积公式可得:三角形ABN和三角形CBM的面积相等,都等于这个正方形的面积的
,据此不难得出三角形AMO和三角形CNO面积相等;且根据高一定时三角形的面积与底成正比例的性质,可得三角形AMO和三角形BMO的面积相等,所以可得:图形中涂色的是个小三角形的面积都相等,据此可求出其中一个小三角形的面积,则用正方形的面积减去这四个小三角形的面积,即可得出四边形AOCD的面积.

| 1 |
| 4 |

解答:解:根据题干分析可得,因为M、N分别为AB边与BC边的中点,
所以三角形ABN=三角形CBM的面积=正方形的面积×
=9×9×
=
(平方厘米),
又因为三角形AMO的面积=三角形CNO面积;且三角形AMO的面积=三角形BMO的面积,
不难得出:四个小三角形的面积相等,所以其中一个小三角形的面积是:
÷3=
(平方厘米),
所以四边形AOCD的面积是:9×9-
×4=81-27=54(平方厘米),
答:四边形AOCD的面积是54平方厘米.
所以三角形ABN=三角形CBM的面积=正方形的面积×
| 1 |
| 4 |
| 1 |
| 4 |
| 81 |
| 4 |
又因为三角形AMO的面积=三角形CNO面积;且三角形AMO的面积=三角形BMO的面积,
不难得出:四个小三角形的面积相等,所以其中一个小三角形的面积是:
| 81 |
| 4 |
| 27 |
| 4 |
所以四边形AOCD的面积是:9×9-
| 27 |
| 4 |
答:四边形AOCD的面积是54平方厘米.
点评:此题考查了高一定时,三角形的面积与底成正比的关系的灵活应用,解答此题的关键是推理得出四个小三角形的面积相等.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
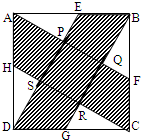 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.