题目内容
3.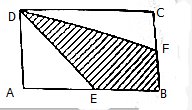 图中长方形的长是20厘米,宽是12厘米,E是AB边上的中点,F是BC边上的中点,求阴影部分的面积.
图中长方形的长是20厘米,宽是12厘米,E是AB边上的中点,F是BC边上的中点,求阴影部分的面积.
分析 首先根据长方形的面积=长×宽,求出长方形ABCD的面积是多少平方厘米;然后根据三角形的面积=底×高÷2,分别求出△ADE、△CDF的面积各是多少;最后用长方形ABCD的面积减去△ADE、△CDF的面积和,求出阴影部分的面积是多少即可.
解答 解:因为E是AB边上的中点,F是BC边上的中点,
所以AE=20÷2=10(厘米),CF=12÷2=6(厘米),
所以阴影部分的面积是:
20×12-12×10÷2-20×6÷2
=240-60-60
=120(平方厘米)
答:阴影部分的面积是120平方厘米.
点评 此题主要考查了组合图形的面积的求法,要熟练掌握,解答此题的关键是要明确长方形、三角形的面积的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.直接写出得数
| 420÷60= | 120÷30= | 240÷80= | 80÷40= |
| 240÷30= | 630÷90= | 350÷70= | 480÷80= |
| 130-50= | 400÷50= | 720÷90= | 330÷30= |
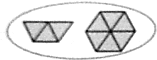 表示1,那么
表示1,那么 表示的分数是$\frac{1}{9}$.
表示的分数是$\frac{1}{9}$.