题目内容
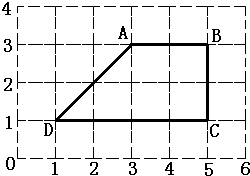 如图所示的是每小格为1×1的正方形面积.(单位:厘米)
如图所示的是每小格为1×1的正方形面积.(单位:厘米)
①如果A的位置用(3,3)表示,那么B、C、D的位置分别是:B(________,________);C(________,________);D(________,________).
②请把图中的梯形划分成面积比是1:2:3的三个三角形,按顺序标出三角形①,②,③.并计算出这个梯形的面积是多少平方厘米?
5 3 5 1 1 1
分析:(1)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,即可解答;
(2)观察图形可知,这个梯形的上底是2厘米,下底是4厘米,高是2厘米,据此利用梯形的面积公式进行计算即可解答;
根据高一定时,三角形的面积与底成正比例的性质,即可将这个梯形的上下底之和,按照1:2:3进行划分,即可解答.
解答:(1)B、C、D的位置分别是:B(5,3);C(5,1);D(1,1);
(2)梯形的面积是:(2+4)×2÷2=6(平方厘米),
将这个梯形按照1:2:3划分如下:

故答案为:5;3;5;1;1;1.
点评:此题主要考查数对表示位置的方法以及根据高一定时、三角形的面积与底成正比例的性质的灵活应用.
分析:(1)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,即可解答;
(2)观察图形可知,这个梯形的上底是2厘米,下底是4厘米,高是2厘米,据此利用梯形的面积公式进行计算即可解答;
根据高一定时,三角形的面积与底成正比例的性质,即可将这个梯形的上下底之和,按照1:2:3进行划分,即可解答.
解答:(1)B、C、D的位置分别是:B(5,3);C(5,1);D(1,1);
(2)梯形的面积是:(2+4)×2÷2=6(平方厘米),
将这个梯形按照1:2:3划分如下:

故答案为:5;3;5;1;1;1.
点评:此题主要考查数对表示位置的方法以及根据高一定时、三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
相关题目

 如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积.
如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积.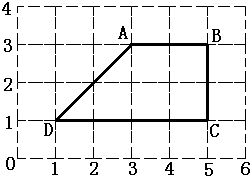 如图所示的是每小格为1×1的正方形面积.(单位:厘米)
如图所示的是每小格为1×1的正方形面积.(单位:厘米)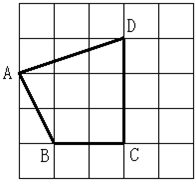 如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积.
如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积.