题目内容
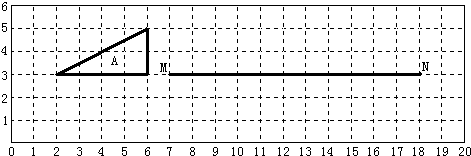
 (2012?宜良县)图中,平行四边形的面积是分成3个三角形,图中甲、乙、丙三个三角形的面积比是
(2012?宜良县)图中,平行四边形的面积是分成3个三角形,图中甲、乙、丙三个三角形的面积比是5:2:3
5:2:3
.分析:由图知:平行四边形的面积是分成3个三角形,图中三个三角形的高都相等,都是平行四边形的高,设为h,甲的底是平行四边形的边,即乙和丙的底的和,根据三角形的面积公式是:底×高÷2,能分别表示出甲、乙、丙3个三角形的面积,从而算出它们面积的比.
解答:解:因为甲、乙、丙三个三角形的高相等,即平行四边形的高,设为h,
又因为甲的底是平行四边形的边,即乙和丙的底的和:2+3=5,
所以甲的面积=5h÷2=
h,
乙的面积=2h÷2=h,
丙的面积=3h÷2=
h,
所以:甲:乙:丙=
h:h:
h=5:2:3.
答;甲、乙、丙三个三角形的面积比是 5:2:3.
故答案填5:2:3.
又因为甲的底是平行四边形的边,即乙和丙的底的和:2+3=5,
所以甲的面积=5h÷2=
| 5 |
| 2 |
乙的面积=2h÷2=h,
丙的面积=3h÷2=
| 3 |
| 2 |
所以:甲:乙:丙=
| 5 |
| 2 |
| 3 |
| 2 |
答;甲、乙、丙三个三角形的面积比是 5:2:3.
故答案填5:2:3.
点评:此题主要考察了三角形面积算法和平行四边形的特点,以及图中平行四边形与三角形底和高的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 (2012?宜良县)把一个底面半径6厘米、高8厘米的圆柱体,切拼成一个近似的长方体,表面积比原来增加了
(2012?宜良县)把一个底面半径6厘米、高8厘米的圆柱体,切拼成一个近似的长方体,表面积比原来增加了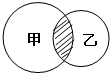 (2012?宜良县)如图,阴影部分的面积相当于甲圆面积的
(2012?宜良县)如图,阴影部分的面积相当于甲圆面积的