题目内容
如图,在一组平行线之间作了一个半圆和一个三角形,问:阴影部分甲与阴影部分乙的面积相差多少?(π取3.14)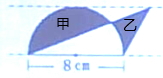

分析:半圆内的阴影部分甲的面积=半圆的面积-扇形面积,右边阴影部分乙的面积=三角形面积-扇形面积,因为夹在平行线间的距离相等,所以三角形的高等于圆的半径,所以:甲的面积-乙的面积=半圆的面积-扇形面积-(三角形面积-扇形面积)=半圆的面积-扇形面积-三角形面积+扇形面积=半圆的面积-三角形面积=
π(8÷2)2-8×(8÷2)÷2,计算即可.
| 1 |
| 2 |
解答:解:如图:
甲的面积-乙的面积,
=
π(8÷2)2-8×(8÷2)÷2,
=3.14×
×16-8×4÷2,
=25.12-16,
=9.12(平方厘米).
答:阴影部分甲与阴影部分乙的面积相差9.12平方厘米.

甲的面积-乙的面积,
=
| 1 |
| 2 |
=3.14×
| 1 |
| 2 |
=25.12-16,
=9.12(平方厘米).
答:阴影部分甲与阴影部分乙的面积相差9.12平方厘米.
点评:解决本题的关键是借助三角形和半圆形表示出2个阴影部分的面积,再相减,得出甲的面积-乙的面积=半圆的面积-三角形面积,再计算即可.

练习册系列答案
相关题目
