题目内容
18.计算:[2$\frac{1}{3}$+(5.4-3$\frac{2}{3}$)×1$\frac{2}{3}$]÷3$\frac{4}{9}$;
(1+$\frac{1}{2}$)×(1-$\frac{1}{2}$)×(1+$\frac{1}{3}$)×(1-$\frac{1}{3}$)×…×(1+$\frac{1}{99}$)×(1-$\frac{1}{99}$)
分析 ①本题主要运用乘法的分配律及分数小数的四则混合运算进行计算,先算小括号内部的,再算括号外部的,即可求值;
②先计算出括号里算式的结果,然后约去互为倒数的分数,最后剩下$\frac{1}{2}×\frac{100}{99}$,据此解答即可.
解答 解:①[2$\frac{1}{3}$+(5.4-3$\frac{2}{3}$)×1$\frac{2}{3}$]÷3$\frac{4}{9}$
=[2$\frac{1}{3}$+5.4×$\frac{5}{3}$-$\frac{11}{3}$×$\frac{5}{3}$]$÷\frac{31}{9}$
=[2$\frac{1}{3}$+9$-\frac{55}{9}$]$÷\frac{31}{9}$
=[$\frac{21}{9}$$+\frac{81}{9}$$-\frac{55}{9}$]×$\frac{9}{31}$
=$\frac{47}{9}$×$\frac{9}{31}$
=1$\frac{16}{31}$
②(1+$\frac{1}{2}$)×(1-$\frac{1}{2}$)×(1+$\frac{1}{3}$)×(1-$\frac{1}{3}$)×…×(1+$\frac{1}{99}$)×(1-$\frac{1}{99}$)
=$\frac{3}{2}$×$\frac{1}{2}$×$\frac{4}{3}$×$\frac{2}{3}$×…×$\frac{100}{99}$×$\frac{98}{99}$
=$\frac{1}{2}$×$\frac{100}{99}$
=$\frac{50}{99}$
点评 ①本题主要考查了分数的四则混合运算及乘法的分配律;
②解答本题的关键是用分数表示出每个括号里算式的结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.5:3的后项加上6,要是比值不变,前项应该( )
| A. | 加6 | B. | 乘6 | C. | 乘3 |
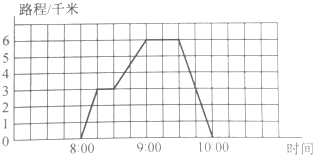 小红骑车到离家6千米的一个风景区游玩,请根据下面的折线图回答问题.
小红骑车到离家6千米的一个风景区游玩,请根据下面的折线图回答问题.