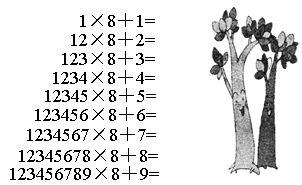题目内容
用计算器探索规律.
(1)11×11=
111×111=
1111×1111=
11111×11111=…
根据上面的规律推算:
×
=
(2)11×9=
222×9=
3333×9=
44444×9=
根据上面的规律推算:
5555555×9=
×9=
(1)11×11=
111×111=
1111×1111=
11111×11111=…
根据上面的规律推算:
| ||
| 9个1 |
| ||
| 9个1 |
(2)11×9=
222×9=
3333×9=
44444×9=
根据上面的规律推算:
5555555×9=
| ||
| 1005个8 |
分析:(1)通过计算得出规律:其中一个因数中有几个1,则结果正中间的数就是几,左边依次递增,右边依次递减,依此即可计算;
(2)通过计算,得出规律:第一个因数里面有n个数字,那么积的左起第一个数字从第二个算式起,每个算式得数的最高位上依次是1、2、3、4、5、…;中间连续是(n-1)个9,最后一个数字依次是9、8、7、…,依次减少1个;据此解答即可.
(2)通过计算,得出规律:第一个因数里面有n个数字,那么积的左起第一个数字从第二个算式起,每个算式得数的最高位上依次是1、2、3、4、5、…;中间连续是(n-1)个9,最后一个数字依次是9、8、7、…,依次减少1个;据此解答即可.
解答:解:(1)11×11=121;
111×111=12321;
1111×1111=1234321;
11111×11111=123454321;
规律:得数前几位是从1开始的连续自然数,直到最中间的数等于其中一个因数里面1的个数,然后再顺次倒数到1即可.
根据上面的规律推算:
×
=12345678987654321;
(2)11×9=99;
222×9=1998;
3333×9=29997;
44444×9=399996;
规律:得数前几位是从1开始的连续自然数,直到最中间的数等于其中一个因数里面1的个数,然后再顺次倒数到1;
根据上面的规律推算:
5555555×9=49999995;
×9=7
2;
故答案为:(1)121;12321;1234321;123454321;12345678987654321;
(2)99;1998;29997;399996;49999995;7
2.
111×111=12321;
1111×1111=1234321;
11111×11111=123454321;
规律:得数前几位是从1开始的连续自然数,直到最中间的数等于其中一个因数里面1的个数,然后再顺次倒数到1即可.
根据上面的规律推算:
| ||
| 9个1 |
| ||
| 9个1 |
(2)11×9=99;
222×9=1998;
3333×9=29997;
44444×9=399996;
规律:得数前几位是从1开始的连续自然数,直到最中间的数等于其中一个因数里面1的个数,然后再顺次倒数到1;
根据上面的规律推算:
5555555×9=49999995;
| ||
| 1005个8 |
| ||
| 1004个9 |
故答案为:(1)121;12321;1234321;123454321;12345678987654321;
(2)99;1998;29997;399996;49999995;7
| ||
| 1004个9 |
点评:解决本题的关键是先根据个别算式计算找出规律,再利用规律解答.

练习册系列答案
相关题目