题目内容
有一组图,它的排列规律是: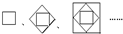 第四个图形中有________个三角形;第n个图形中有________个三角形.
第四个图形中有________个三角形;第n个图形中有________个三角形.
12 (n-1)×4
分析:结合图形至少数出前三个图形中三角形的个数,然后发现规律:后一个图形中三角形的个数总比前一个图形中三角形的个数多4.因为第一个图形三角形的个数为0,第二个图形三角形的个数为4,往下依次多4个三角形,从而推出第n个图形中三角形的个数是(n-1)×4.
解答:(1)结合图形不难发现:后一个图形中三角形的个数总比前一个图形中三角形的个数多4,
(2)根据(1)中的发现,运用字母表示即可.故在第n个图形中三角形的个数是(n-1)×4.
故答案为:12,(n-1)×4.,
点评:本题主要考查通过图形的变化找规律,注意由特殊到一般的归纳方法.
分析:结合图形至少数出前三个图形中三角形的个数,然后发现规律:后一个图形中三角形的个数总比前一个图形中三角形的个数多4.因为第一个图形三角形的个数为0,第二个图形三角形的个数为4,往下依次多4个三角形,从而推出第n个图形中三角形的个数是(n-1)×4.
解答:(1)结合图形不难发现:后一个图形中三角形的个数总比前一个图形中三角形的个数多4,
(2)根据(1)中的发现,运用字母表示即可.故在第n个图形中三角形的个数是(n-1)×4.
故答案为:12,(n-1)×4.,
点评:本题主要考查通过图形的变化找规律,注意由特殊到一般的归纳方法.

练习册系列答案
相关题目
 (2004?长汀县)有一组图,它的排列规律如下图所示,请你画出这组图中的第(6)个图.
(2004?长汀县)有一组图,它的排列规律如下图所示,请你画出这组图中的第(6)个图.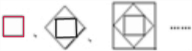 第四个图形中有
第四个图形中有 有一组图,它的排列规律如下图所示,请你画出这组图中的第(6)个图.
有一组图,它的排列规律如下图所示,请你画出这组图中的第(6)个图.