题目内容
在1、2、3、…、30这30个自然数中,最多能取出
15
15
个数,使取出的数中,任意两个不同的数的和都不是7的倍数.分析:将1、2、3…29、30按除以7的余数分成以下几类:
①{1,8,15,22,29},②{2,9,16,23,30},③{3,10,17,24},④{4,11,18,25},⑤{5,12,19,26},⑥{6,13,20,27},⑦{7,14,21,28}.发现这几组数的特点:
①和⑥中两数之和是7的倍数,②和⑤中两数之和是7的倍数,③和④中两数之和是7的倍数;
考虑极端情况:将前3组数全部取完,和第7组一个数,共5+5+4+1=15个,(后面三组与第7组一个数共4+4+4+1=13个),这15个(13个)数中任意两个不同的数的和都不是7的倍数.若再多到一个,则这一个数必然与前四组中某一个数的和是7的倍数.
①{1,8,15,22,29},②{2,9,16,23,30},③{3,10,17,24},④{4,11,18,25},⑤{5,12,19,26},⑥{6,13,20,27},⑦{7,14,21,28}.发现这几组数的特点:
①和⑥中两数之和是7的倍数,②和⑤中两数之和是7的倍数,③和④中两数之和是7的倍数;
考虑极端情况:将前3组数全部取完,和第7组一个数,共5+5+4+1=15个,(后面三组与第7组一个数共4+4+4+1=13个),这15个(13个)数中任意两个不同的数的和都不是7的倍数.若再多到一个,则这一个数必然与前四组中某一个数的和是7的倍数.
解答:解:根据题干分析可得:
最多为5+5+4+1=15(个),
答:最多能取出15个数,使取出的数中,任意两个不同的数的和都不是7的倍数.
故答案为:15.
最多为5+5+4+1=15(个),
答:最多能取出15个数,使取出的数中,任意两个不同的数的和都不是7的倍数.
故答案为:15.
点评:此题抓住数的整除的特征,利用余数特点将这些数字进行分类从而解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
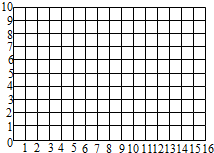 (1)在下面方格图中画一个直角三角形,已知三角形的两个锐角的顶点,分别在A(2、3),B(4、5)的位置上,那么直角的顶点C的位置可以是
(1)在下面方格图中画一个直角三角形,已知三角形的两个锐角的顶点,分别在A(2、3),B(4、5)的位置上,那么直角的顶点C的位置可以是