题目内容
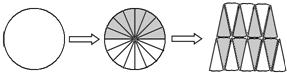
【题目】圆的面积公式推导，教材上是将圆转化成近似的长方形，从而推导出圆面积计算公式，我们也可以将圆转化为近似的三角形或梯形，从而推导出圆面积的计算公式，请你仔细观察，动脑试试：将圆沿直径平均分成16个小扇形，用如图（圆的半径为r）所示的方法，可以拼成一个近似的梯形，梯形的上底等于圆的 ，梯形的下底等于圆的 ，梯形的高等于圆的 ．因为梯形的面积= ，所以圆的面积等于 ．
【答案】周长的
，周长的
，半径的2倍，（上底+下底）×高÷2，πr2．
【解析】
试题分析：将圆沿直径平均分成16个小扇形，用如图（圆的半径为r）所示的方法，可以拼成一个近似的梯形，把圆转化成一个近似的梯形，梯形的上底加下底的和相当于圆周长的
，梯形的高相当于圆半径的2倍，梯形的面积等于上底加下底的和乘高除以2，所以圆的面积=2πr××2r÷2=πr2；据此解答．
解：将圆沿直径平均分成16个小扇形，用如图（圆的半径为r）所示的方法，可以拼成一个近似的梯形，
梯形的上底等于圆的周长的，梯形的下底等于圆的周长的，即梯形的上底加下底的和等于圆周长的，梯形的高等于圆的半径的2倍．
因为梯形的面积=（上底+下底）×高÷2，
所以圆的面积=2πr××2r÷2=πr2；
故答案为：周长的，周长的，半径的2倍，（上底+下底）×高÷2，πr2．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
