题目内容
 如图中的圆是以O为圆心、半径是10厘米的圆,求阴影部分的面积.
如图中的圆是以O为圆心、半径是10厘米的圆,求阴影部分的面积.分析:由图意可知:阴影部分的面积=半径为10厘米的圆面积的
-(半径为AC的
圆的面积-三角形ABC的面积),又因AB=20厘米,OC=10厘米,从而可以依据三角形ABC的面积求出AC的长度,进而求得阴影部分的面积.
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:三角形ABC的面积为:所以AC2÷2=AB×OC÷2=10×2×10÷2=100(平方厘米),
由上面计算可得:AC2=100×2=200,
所以阴影部分的面积是:3.14×10×10÷2-(
×3.14×200-100),
=157-(157-100),
=157-57,
=100(平方厘米),
答:阴影部分的面积是100平方厘米.
由上面计算可得:AC2=100×2=200,
所以阴影部分的面积是:3.14×10×10÷2-(
| 1 |
| 4 |
=157-(157-100),
=157-57,
=100(平方厘米),
答:阴影部分的面积是100平方厘米.
点评:此题考查圆的面积与扇形的面积公式的灵活应用,关键是根据三角形ABC的面积得出AC2的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ①如图,O是直线上的一点,请过O点画出已知直线的垂线.
①如图,O是直线上的一点,请过O点画出已知直线的垂线. 如图,以等腰直角三角形的中位线(两条边中点的连线)的中点O为圆心,以高长的一半为半径画一个圆,交两边于E、F,那么,图中阴影部分的面积是多少?(单位:cm)
如图,以等腰直角三角形的中位线(两条边中点的连线)的中点O为圆心,以高长的一半为半径画一个圆,交两边于E、F,那么,图中阴影部分的面积是多少?(单位:cm)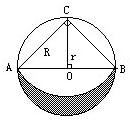 如图中的圆是以O为圆心、半径是10厘米的圆,求阴影部分的面积.
如图中的圆是以O为圆心、半径是10厘米的圆,求阴影部分的面积.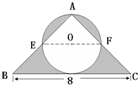 如图,以等腰直角三角形的中位线(两条边中点的连线)的中点O为圆心,以高长的一半为半径画一个圆,交两边于E、F,那么,图中阴影部分的面积是多少?(单位:cm)
如图,以等腰直角三角形的中位线(两条边中点的连线)的中点O为圆心,以高长的一半为半径画一个圆,交两边于E、F,那么,图中阴影部分的面积是多少?(单位:cm)