题目内容
 如图,圆内线段AB把圆周分成两段弧,已知弧ACB与弧ADB的长度之比为1:3,圆的半径是6厘米,那么圆中阴影部分的面积是
如图,圆内线段AB把圆周分成两段弧,已知弧ACB与弧ADB的长度之比为1:3,圆的半径是6厘米,那么圆中阴影部分的面积是10.26
10.26
平方厘米.(π取3.14)分析:由题意可知:弧ACB与弧ADB的长度之比为1:3,则它们所对应的圆心角的度数比也为1:3,把整个圆周的度数看作单位“1”,∠AOB的度数就占圆周度数的
,又因圆周的度数为360度,从而可以求出∠AOB的度数,再据“阴影部分的面积=扇形AOB的面积-三角形AOB的面积”即可求解.
| 1 |
| 1+3 |
解答:解:∠AOB=360°×
=90°,
所以三角形AOB就是等腰直角三角形,
扇形AOB的面积=
圆的面积,
阴影部分的面积为:
×3.14×62-6×6÷2,
=
×3.14×36-18,
=3.14×9-18,
=28.26-18,
=10.26(平方厘米);
答:阴影部分的面积是10.26平方厘米.
故答案为:10.26.
| 1 |
| 1+3 |
所以三角形AOB就是等腰直角三角形,
扇形AOB的面积=
| 1 |
| 4 |
阴影部分的面积为:
| 1 |
| 4 |
=
| 1 |
| 4 |
=3.14×9-18,
=28.26-18,
=10.26(平方厘米);
答:阴影部分的面积是10.26平方厘米.
故答案为:10.26.
点评:推论得出三角形AOB是等腰直角三角形,是解答本题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
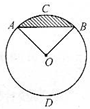 如图,圆内线段AB把圆周分成两段弧,已知弧ACB与弧ADB的长度之比为1:3,圆的半径是6厘米,那么圆中阴影部分的面积是________平方厘米.(π取3.14)
如图,圆内线段AB把圆周分成两段弧,已知弧ACB与弧ADB的长度之比为1:3,圆的半径是6厘米,那么圆中阴影部分的面积是________平方厘米.(π取3.14)