题目内容
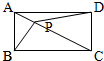
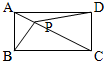如图：P是矩形ABCD内任意一点，连接PA、PB、PC、PD，则三角形PAD的面积与三角形PBC的面积之和与三角形PAB的面积与三角形PCD的面积之和相等．
正确
分析：根据同底等高的三角形面积相等，可得三角形PAD的面积=三角形PAB的面积，三角形PCD的面积=三角形PBC的面积，再根据等式的性质即可作出判断．
解答：观察图形可知，三角形PAD的面积=三角形PAB的面积，三角形PCD的面积=三角形PBC的面积，
则三角形PAD的面积+三角形PBC的面积=三角形PAB的面积+三角形PCD的面积，
故答案为：√．
点评：考查了三角形的面积，本题关键是掌握等底等高的三角形面积相等的性质．
分析：根据同底等高的三角形面积相等，可得三角形PAD的面积=三角形PAB的面积，三角形PCD的面积=三角形PBC的面积，再根据等式的性质即可作出判断．
解答：观察图形可知，三角形PAD的面积=三角形PAB的面积，三角形PCD的面积=三角形PBC的面积，
则三角形PAD的面积+三角形PBC的面积=三角形PAB的面积+三角形PCD的面积，
故答案为：√．
点评：考查了三角形的面积，本题关键是掌握等底等高的三角形面积相等的性质．
练习册系列答案
相关题目
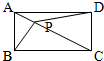如图：P是矩形ABCD内任意一点，连接PA、PB、PC、PD，则三角形PAD的面积与三角形PBC的面积之和与三角形PAB的面积与三角形PCD的面积之和相等．