Question

数学小知识： “勾股定理”是指在一个直角三角形中，两条直角边的平方和等于斜边的平方．例如：两条直角边的长分别为3、4，则32+42= 52，即斜边的长为5．

已知图中两条直角边的长度，求出图中以斜边为直径所作圆的面积．

Answer 1

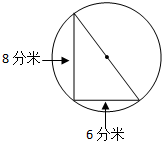
解：设这个圆的半径为r，则直径就是2r，根据勾股定理可得：
（2r）²=8²+6²，
4r²=64+36，
4r²=100，
r²=25，
所以r=5；
3.14×5²，
=3.14×25，
=78.5（平方分米）；
答：这个圆的面积是78.5平方分米．
分析：设这个圆的半径为r，则直径就是2r，根据勾股定理可得：（2r）²=8²+6²由此设出这个圆的半径即可求出这个圆的面积．
点评：此题考查了圆的面积公式的计算应用以及利用勾股定理求直角三角形的斜边的计算方法．