Question

【题目】甲班与乙班学生同时从学校出发去公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使两班学生在最短时间内到达公园，那么甲班学生与乙班学生需要步行的距离之比是多少？

Answer 1

【答案】15:11

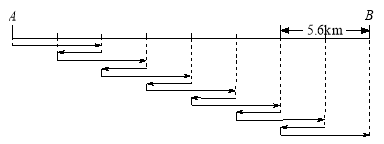
【解析】方法一：不妨设乙班学生先步行，汽车将甲班学生送至A地后返回，在B处接到乙班学生，最后汽车与乙班学生同时到达公园，如图：

：=1：12，：=1：16。乙班从C至B时，汽车从C~A~B，则两者路程之比为1：16，不妨设CB=1，则C~A~B=16，CA=（1＋16）÷2=8.5，则有CB：BA=1:7.5；类似设AD=1，分析可得AD:BA=1:5.5，综合得CB:BA：AD=22:165：30，说明甲乙两班步行的距离之比是15:11。

方法二：如图，假设实线代表汽车行驶的路线，虚线代表甲班和乙班行走的路线，假设乙班行驶份到达点，则汽车行驶份到达点，汽车与乙班共行驶份在点相遇，其中乙班步行了份，同时甲班步行了份，此时汽车与甲班相差份，这样甲班还需步行份，所以甲班与乙班步行的路程比为

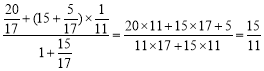
方法三：由于汽车速度是甲班速度的倍，是乙班速度的倍，设乙班步行份，则汽车载甲班学生到点返回与乙班相遇，共行份，所以，类似的设甲班步行份，则汽车从点返回到点又与甲班同时到达点，所以,，所以,所以甲班与乙班步行的路程比为