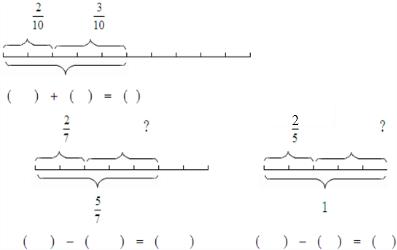
题目内容
12.如图,梯形的上底为a,下底长为b,高为h,证明梯形的面积S梯=$\frac{1}{2}$(a+b)h(用三种方法证明)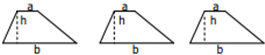
分析 第一种,如图一:从A和D分别向BC边作垂线,那么梯形面积就是两个三角形加中间的矩形,三角形面积和矩形面积相加就得出结果,矩形面积=a×h,假设两个三角形的底分别为e,f,那么面积是$\frac{1}{2}$(e×h),$\frac{1}{2}$(f×h),而e+f=b-a相加,面积=a×h+$\frac{1}{2}$(e×h)+$\frac{1}{2}$(f×h)=$\frac{1}{2}$(a+b)h;
第二种,如图二:从A向BC变作平行于CD的线,那么梯形面积就是三角形加平行四边形面积
平行四边形面积=a×h,三角形面积=$\frac{1}{2}$(b-a)h,相加=$\frac{1}{2}$(a+b)h;
第三种,如图三:连接AC,梯形面积就是两个三角形面积相加.两个三角形面积分别为:$\frac{1}{2}$ah,$\frac{1}{2}$bh,相加=$\frac{1}{2}$(a+b)h.
解答 解:证明(1)如图一:从A和D分别向BC边作垂线交BC于E和F,设BE=e,CF=f,
三角形ABE和三角形DCF的高:AE=DF=h,
因为三角形ABE的面积=$\frac{1}{2}$e×h,三角形DCF的面积=$\frac{1}{2}$f×h,矩形面积=a×h,e+f=b-a,
所以梯形ABCD的面积=三角形ABE的面积+矩形AEFD的面积+三角形DCF的面积=$\frac{1}{2}$e×h+a×h+$\frac{1}{2}$f×h=$\frac{1}{2}$(e+f)h+a×h=$\frac{1}{2}$(b-a)h+ah=$\frac{1}{2}$(a+b)h
证明(2)如图二:从A和D分别向BC边作垂线交BC于E和F,从A向BC作平行于CD的线,交BC于G,则GC=AD=a,
三角形ABG和平行四边形AGCD的高:AE=DF=h,BG=b-a,
因为平行四边形AGCD的面积=a×h,三角形ABG的面积=$\frac{1}{2}$(b-a)h,
所以梯形ABCD的面积=平行四边形AGCD的面积+三角形ABG的面积=a×h+$\frac{1}{2}$(b-a)h=$\frac{1}{2}$(a+b)h
证明(3)如图三:从A向BC边作垂线交BC于E,从C向AD作垂线交AD的延长线于F,连接AC,
则三角形ABC的高和三角形CDA的高:AE=CF=h,
因为三角形ABC的面积=$\frac{1}{2}$b×h,三角形ACD的面积=$\frac{1}{2}$a×h,
所以梯形ABCD的面积=三角形ABC的面积+三角形ACD的面积=$\frac{1}{2}$b×h+$\frac{1}{2}$a×h=$\frac{1}{2}$(a+b)h
点评 此题主要考查梯形的面积公式推导的方法.