题目内容
| 解方程.你是最细心的! x-0.25=0.25 |
4+0.7x=102 | 3x-16×3=102 | ||||||||||
x-
|
1-
|
| ||||||||||
|
x×(1-
|
|
分析:(1)根据等式的基本性质在方程的两边同时加上0.25求解即可;
(2)先根据等式的基本性质在方程的两边同时减去4,然后在方程的两边同时除以0.7求解即可;
(3)先计算16×3得48,然后根据等式的基本性质在方程的两边同时加上48,最后方程两边同时除以3求解即可;
(4)先把方程左边合并,然后根据等式的基本性质在方程的两边同时除以
求解即可;
(5)先根据等式的基本性质在方程的两边同时加上
X,再求解即可;
(6)根据等式的基本性质在方程的两边同时除以
求解即可;
(7)先根据比例的基本性质,把比例化成方程,然后再根据等式的基本性质在方程的两边同时除以
求解即可;
(8)先化简方程的左边,然后根据等式的基本性质在方程的两边同时除以
求解即可;
(9)先根据比例的基本性质,把比例化成方程,然后再根据等式的基本性质在方程的两边同时除以2求解即可.
(2)先根据等式的基本性质在方程的两边同时减去4,然后在方程的两边同时除以0.7求解即可;
(3)先计算16×3得48,然后根据等式的基本性质在方程的两边同时加上48,最后方程两边同时除以3求解即可;
(4)先把方程左边合并,然后根据等式的基本性质在方程的两边同时除以
| 3 |
| 4 |
(5)先根据等式的基本性质在方程的两边同时加上
| 3 |
| 4 |
(6)根据等式的基本性质在方程的两边同时除以
| 1 |
| 4 |
(7)先根据比例的基本性质,把比例化成方程,然后再根据等式的基本性质在方程的两边同时除以
| 1 |
| 3 |
(8)先化简方程的左边,然后根据等式的基本性质在方程的两边同时除以
| 5 |
| 8 |
(9)先根据比例的基本性质,把比例化成方程,然后再根据等式的基本性质在方程的两边同时除以2求解即可.
解答:解:(1)x-0.25=0.25,
x-0.25+0.25=0.25+0.25,
x=0.5;
(2)4+0.7x=102,
4+0.7x-4=102-4,
0.7x=98,
0.7x÷0.7=98÷0.7,
x=140;
(3)3x-16×3=102,
3x-48=102,
3x-48+48=102+48,
3x=150,
3x÷3=150÷3,
x=50;
(4)x-
x=
,
x=
,
x÷
=
÷
,
x=
;
(5)1-
x=
,
1-
x+
x=
+
x,
+
x=1,
+
x-
=1-
,
x=
,
x÷
=
÷
,
x=
;
(6)
=30%,
÷
=30%÷
,
x=
;
(7)
:0.25=80%:x,
x=0.25×80%,
x=0.2,
x÷
=0.2÷
,
x=0.6;
(8)x×(1-
)=1
,
x=1
,
x÷
=1
÷
,
x=
;
(9)
=
,
2x=10×0.1,
2x=1,
2x÷2=1÷2,
x=
.
x-0.25+0.25=0.25+0.25,
x=0.5;
(2)4+0.7x=102,
4+0.7x-4=102-4,
0.7x=98,
0.7x÷0.7=98÷0.7,
x=140;
(3)3x-16×3=102,
3x-48=102,
3x-48+48=102+48,
3x=150,
3x÷3=150÷3,
x=50;
(4)x-
| 1 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
x=
| 1 |
| 2 |
(5)1-
| 3 |
| 4 |
| 3 |
| 5 |
1-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 4 |
| 2 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 5 |
| 3 |
| 4 |
x=
| 8 |
| 15 |
(6)
| x |
| 4 |
| x |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
x=
| 6 |
| 5 |
(7)
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
x=0.6;
(8)x×(1-
| 3 |
| 8 |
| 2 |
| 3 |
| 5 |
| 8 |
| 2 |
| 3 |
| 5 |
| 8 |
| 5 |
| 8 |
| 2 |
| 3 |
| 5 |
| 8 |
x=
| 8 |
| 3 |
(9)
| x |
| 10 |
| 0.1 |
| 2 |
2x=10×0.1,
2x=1,
2x÷2=1÷2,
x=
| 1 |
| 2 |
点评:此题考查了根据等式的性质以及比例的基本性质解方程.

练习册系列答案
相关题目
 x=
x=
 x=
x=
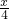 =30%
=30% :0.25=80%:x
:0.25=80%:x
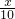 =
=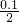 .
.