题目内容
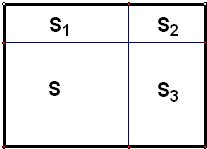 一个大长方形被分成三个小长方形S1、S2、S3和一个正方形S,已知S1与S2的面积和为13,S2与S3的面积和为33,每个小长方形的长和宽都是正整数,且正方形的面积比小长方形S1、S2、S3的面积都大,则正方形的面积为
一个大长方形被分成三个小长方形S1、S2、S3和一个正方形S,已知S1与S2的面积和为13,S2与S3的面积和为33,每个小长方形的长和宽都是正整数,且正方形的面积比小长方形S1、S2、S3的面积都大,则正方形的面积为100
100
.分析:设正方形S的边长是a,S1的边长是a和x,S3的边长是a和y,则由题意得:x (a+y)=13,y (a+x)=33,因为每个小长方形的长和宽都是正整数所以a和x、y都是正整数,所以由x (a+y)=13,1×13=13,得:x=1,a+y=13,由y (a+x)=33得出3×11=33,得:y=3,a+x=11从而a=10,据此计算出正方形的面积.
解答:解:设正方形S的边长是a,S1的边长是a和x,
S3的边长是a和y,
则由题意得:x (a+y)=13,y (a+x)=33,
因为每个小长方形的长和宽都是正整数,
所以a和x、y都是正整数,
所以由x (a+y)=13=1×13得:x=1,a+y=13,
由y (a+x)=33=3×11得:y=3,a+x=11,
所以a=10,正方形的面积为10×10=100.
故答案为:100.
S3的边长是a和y,
则由题意得:x (a+y)=13,y (a+x)=33,
因为每个小长方形的长和宽都是正整数,
所以a和x、y都是正整数,
所以由x (a+y)=13=1×13得:x=1,a+y=13,
由y (a+x)=33=3×11得:y=3,a+x=11,
所以a=10,正方形的面积为10×10=100.
故答案为:100.
点评:解决此题的关键是S1与S2的面积和为13,S2与S3的面积和为33,由此得出正方形的边长.

练习册系列答案
相关题目
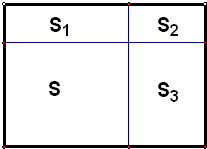 一个大长方形被分成三个小长方形S1、S2、S3和一个正方形S,已知S1与S2的面积和为13,S2与S3的面积和为33,每个小长方形的长和宽都是正整数,且正方形的面积比小长方形S1、S2、S3的面积都大,则正方形的面积为________.
一个大长方形被分成三个小长方形S1、S2、S3和一个正方形S,已知S1与S2的面积和为13,S2与S3的面积和为33,每个小长方形的长和宽都是正整数,且正方形的面积比小长方形S1、S2、S3的面积都大,则正方形的面积为________.