题目内容
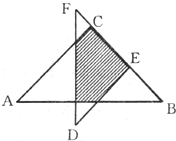 △ABC和△DEF为两个叠放在一起的等腰直角三角形(如图).已知BC=10,CF=1,DE=7.则阴影部分的面积是多少?
△ABC和△DEF为两个叠放在一起的等腰直角三角形(如图).已知BC=10,CF=1,DE=7.则阴影部分的面积是多少?分析:由题意可知:阴影部分的面积=S△FMB-S△FGC-S△HBE;因为FE=DE=7,CF=1,所以CE=7-1=6;因为BC=10,所以BE=10-6=4;有因为S△FMB、S△FGC、S△HBE都是等腰直角三角形;它们的面积都可求出来,从而问题逐步得解.


解答:解:根据分析可知,因为△ABC和△DEF为两个叠放在一起的等腰直角三角形,所以∠FMB=90°,∠FCG=90°,∠BEH=90°,△FBM它的高等于FB的一半;
因为FE=DE=7,CF=1,所以CE=7-1=6;
因为BC=10,所以BE=10-6=4;
FB=FC+BC=1+10=11;
阴影部分的面积:
×11×(11÷2)-
×1×1-
×4×4,
=30.25-0.5-8,
=21.75;
答:阴影部分的面积是21.75.
因为FE=DE=7,CF=1,所以CE=7-1=6;
因为BC=10,所以BE=10-6=4;
FB=FC+BC=1+10=11;
阴影部分的面积:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=30.25-0.5-8,
=21.75;
答:阴影部分的面积是21.75.
点评:解答此题关键是先求出CE和BE的长度,难点是根据等腰直角三角形的高等于斜边长度的一半求出△FBM的高;进而利用阴影部分的面积=S△FMB-S△FGC-S△HBE,即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 两个形状和大小都一样的直角三角形△ABC和△DEF,如图放置,它们的面积都是2003平方厘米,而每一个三角形的顶点恰好都落在另一个三角形的斜边上.这两个直角三角形的重叠部分是一个长方形,那么四边形ADEC的面积为
两个形状和大小都一样的直角三角形△ABC和△DEF,如图放置,它们的面积都是2003平方厘米,而每一个三角形的顶点恰好都落在另一个三角形的斜边上.这两个直角三角形的重叠部分是一个长方形,那么四边形ADEC的面积为