题目内容
 在如图的三角形中画一条线段,将它分成两个三角形,使两个三角形面积的比是1﹕3,并在图上标上相关数据.
在如图的三角形中画一条线段,将它分成两个三角形,使两个三角形面积的比是1﹕3,并在图上标上相关数据.分析:因三角形的面积与底成正比,可量出三角形的一条边的长度,在这长边的
处点上点,连接和它相对的顶点,所分成的两个三角形面积的比就是1:3.据此解答.
| 1 |
| 4 |
解答:解:根据分析画图如下:
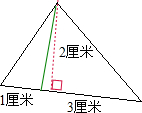
分成后三角形的面积是:
(3+1)×2÷2×
,
=4×2÷2×
,
=1(平方厘米),
(3+1)×2÷2×
,
=4×2÷2×
,
=3(平方厘米).
答:分成后的三角形的面积为分别是1平方厘米,3平方厘米.

分成后三角形的面积是:
(3+1)×2÷2×
| 1 |
| 3+1 |
=4×2÷2×
| 1 |
| 4 |
=1(平方厘米),
(3+1)×2÷2×
| 3 |
| 3+1 |
=4×2÷2×
| 3 |
| 4 |
=3(平方厘米).
答:分成后的三角形的面积为分别是1平方厘米,3平方厘米.
点评:本题的关键是根据三角形的面积与底成正比.从而确定底边分成三角形点的位置.

练习册系列答案
相关题目
 在如图的三角形中画一条线段,把它分成一个钝角三角形和一个锐角三角形.
在如图的三角形中画一条线段,把它分成一个钝角三角形和一个锐角三角形. 在如图的等腰梯形中画一条线段,把它分成一个平行四边形和一个三角形.通过量三角形的边可发现:这是一个
在如图的等腰梯形中画一条线段,把它分成一个平行四边形和一个三角形.通过量三角形的边可发现:这是一个 (1)在如图的三角形中,画出AB边上的高.
(1)在如图的三角形中,画出AB边上的高.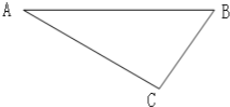 (1)在如图的三角形中,画出AB边上的高.
(1)在如图的三角形中,画出AB边上的高.