题目内容

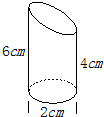最早将圆周率精确地计算到小数点后面7位，请借助圆周率计算立体图形（如图）的侧面积为平方厘米．

祖冲之 31.4
分析：先求出底面直径是2厘米，高是4厘米的圆柱的侧面积；再求出底面直径是2厘米，高是（6-4）厘米的圆柱的侧面积的一半；把两次求出的侧面积合起来即为组合图形的侧面积．
解答：底面直径是2厘米，高是4厘米的圆柱的侧面积：3.14×2×4=25.12（平方厘米），
底面直径是2厘米，高是（6-4）厘米的圆柱的侧面积的一半：3.14×2×（6-4）× $\text{[math]}$ =6.28（平方厘米），
组合图形的侧面积：25.12+6.28=31.4（平方厘米）．
答：立体图形的侧面积为31.4平方厘米．
故答案为：祖冲之，31.4．
点评：解决此题关键是先求出高是4厘米的圆柱的侧面积和高是2厘米的圆柱的侧面积的 $\text{[math]}$ ，两个侧面积之和即为组合图形的侧面积．