题目内容
【题目】如图的网格图中每个小正方形的边长为1cm.
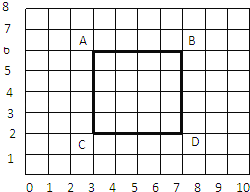
(1)分别以正方形ABCD的四个顶点为圆心,2cm为半径画圆.
(2)在这四个圆与正方形ABCD组合的图形中,共有 条对称轴,这些对称轴的交点位置可以用数对( , )表示.
(3)在这四个圆与正方形ABCD组合的图形中,若将圆与正方形ABCD重叠的部分画上阴影,则该组合图形中空白部分的面积是 cm2.
【答案】如图,2,5,4;53.68.
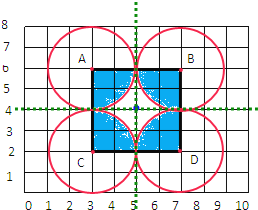
【解析】
试题分析:(1)依据圆的基本画法,分别以正方形ABCD的四个顶点为圆心,2cm为半径,即可画出符合要求的圆;
(2)依据轴对称梯形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,即可得出其对称轴的条数,再据数对表示位置的方法,进行解答即可;
(3)由题意可知:空白部分的面积=3个圆的面积+正方形的面积,利用正方形和圆的面积公式即可求解.
解:(1)据分析画圆如下:

(2)在这四个圆与正方形ABCD组合的图形中,共有2条对称轴,这些对称轴的交点位置可以用数对(5,4)表示.
(3)3.15×22×3+4×4,
=37.68+16,
=53.68(平方厘米);
答:空白部分的面积是53.68平方厘米.
故答案为:2,5,4;53.68.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
