题目内容
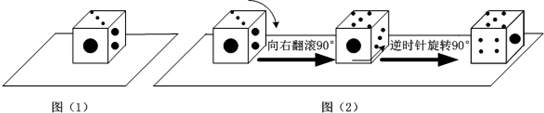
将正方体骰子（相对面上的点数分别是1和6，2和5，3和4）放置于水平桌面上．如图，在图二中，将骰子向右翻滚90°，然后在桌面上，按逆时针方向旋转90°，则完成1次变换．若骰子的初始位置为图一所示状态．那么上述规则连续完成23次变换后．骰子朝上的一面点数是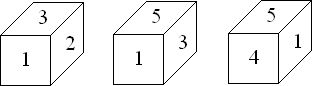
6
6
分析：先向右翻滚，然后再逆时针旋转叫做一次变换，这一次变换的变化：
原来的左面的5移到到上面，原来下面的4移动到了正面，原来正面的1到了右面，原来右面的2到了下面，原来后面6到了左面，原来上面的3到了后面；
再一次变换后：
上面是6，正面是2，下面是1，后面是5，左面是3，右面是4；
第三次变换之后：
上面是3，正面是1，下面是4，后面是6，左面是5，右面是2；这与原来相同；
那么连续3次变换是一个循环．
本题先要找出3次变换是一个循环，然后再求23被3整除后余数是2，从而确定第23次变换后的图形．
原来的左面的5移到到上面，原来下面的4移动到了正面，原来正面的1到了右面，原来右面的2到了下面，原来后面6到了左面，原来上面的3到了后面；
再一次变换后：
上面是6，正面是2，下面是1，后面是5，左面是3，右面是4；
第三次变换之后：
上面是3，正面是1，下面是4，后面是6，左面是5，右面是2；这与原来相同；
那么连续3次变换是一个循环．
本题先要找出3次变换是一个循环，然后再求23被3整除后余数是2，从而确定第23次变换后的图形．
解答：解：根据题意可知连续3次变换是一组循环．
所以23÷3=7（组）…2（次）．
所以是第23次变换，是第8组变换的第2次变换，此时上面的点数是6．
故答案为：6．
所以23÷3=7（组）…2（次）．
所以是第23次变换，是第8组变换的第2次变换，此时上面的点数是6．
故答案为：6．
点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子只能向前或向右翻动．开始时，骰子如图1那样摆放，朝上的点数是2；最后翻动到如图2所示的位置．此时，骰子朝上的点数不可能是下列选项中的（ ）
