Question

高是18.84分米的圆柱，侧面展开是一个正方形，把这个圆柱削成一个最大的长方体，削去部分的体积是________立方厘米．

Answer 1

193.2984
分析：（1）根据圆柱的侧面展开图特点，可知这个圆柱的底面周长是18.84分米，由此即可求得圆柱的底面半径，从而求得圆柱的体积；
（2）要求削去部分的体积，可以先求出削成的这个长方体的体积，这个长方体的底面积就是圆柱的底面上最大的正方形的面积；根据圆内最大正方形的特点即可解决．

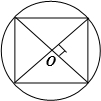
解答：圆柱的底面半径为：18.84÷3.14÷2=3（分米），
3.14×3²×18.84-2×3×3×18.84，
=3.14×9×18.84-18×18.84，
=532.4184-339.12，
=193.2984（立方厘米）；
答：消去部分的体积是193.2984立方厘米．
故答案为：193.2984．
点评：根据圆柱侧面展开图的特点，得出圆柱的底面周长从而求得它的底面半径，利用圆内接最大的正方形特点解决问题．