题目内容
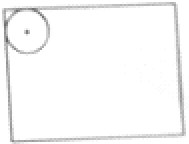 如图是长80厘米,宽60厘米的长方形,它的内侧有一个直径20厘米的圆,沿长方形的边长滚动一周.则圆心经过的总路程是________厘米,圆形滚动不到的地方面积是________平方厘米.(π取3.14)
如图是长80厘米,宽60厘米的长方形,它的内侧有一个直径20厘米的圆,沿长方形的边长滚动一周.则圆心经过的总路程是________厘米,圆形滚动不到的地方面积是________平方厘米.(π取3.14)
200 886
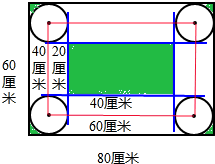
分析:如图所示:(1)由题意可知:圆心经过的图形(红线部分)是一个长和宽分别为(80-20)厘米、(60-20)厘米的长方形,利用长方形的周长公式即可求解.
(2)由图意可知:圆滚动一周,滚不到的面积(绿色部分)是四周的角以及中间的一个小长方形.四周的角合起来相当于一个边长为20厘米的正方形减去一个半径为(20÷2)厘米的圆的面积;中间的小长方形的长为(80-20×2)厘米,宽为(60-20×2),于是问题即可逐步得解.
解答:(1)[(80-20)+(60-20)]×2,
=(60+40)×2,
=100×2,
=200(厘米);
答:圆心经过的总路程是200厘米.
(2)20×20-3.14×(20÷2)2+(80-20×2)×(60-20×2),
=400-314+40×20,
=86+800,
=886(平方厘米);
答:圆形滚动不到的地方面积是886平方厘米.
故答案为:200、886.
点评:解答此题的关键是:弄清楚圆心经过的图形的形状,圆形滚不到的地方由哪几部分组成,从而问题逐步得解.
分析:如图所示:(1)由题意可知:圆心经过的图形(红线部分)是一个长和宽分别为(80-20)厘米、(60-20)厘米的长方形,利用长方形的周长公式即可求解.
(2)由图意可知:圆滚动一周,滚不到的面积(绿色部分)是四周的角以及中间的一个小长方形.四周的角合起来相当于一个边长为20厘米的正方形减去一个半径为(20÷2)厘米的圆的面积;中间的小长方形的长为(80-20×2)厘米,宽为(60-20×2),于是问题即可逐步得解.

解答:(1)[(80-20)+(60-20)]×2,
=(60+40)×2,
=100×2,
=200(厘米);
答:圆心经过的总路程是200厘米.
(2)20×20-3.14×(20÷2)2+(80-20×2)×(60-20×2),
=400-314+40×20,
=86+800,
=886(平方厘米);
答:圆形滚动不到的地方面积是886平方厘米.
故答案为:200、886.
点评:解答此题的关键是:弄清楚圆心经过的图形的形状,圆形滚不到的地方由哪几部分组成,从而问题逐步得解.

练习册系列答案
相关题目
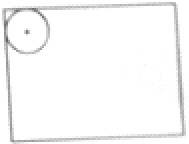 如图是长80厘米,宽60厘米的长方形,它的内侧有一个直径20厘米的圆,沿长方形的边长滚动一周.则圆心经过的总路程是
如图是长80厘米,宽60厘米的长方形,它的内侧有一个直径20厘米的圆,沿长方形的边长滚动一周.则圆心经过的总路程是