Question

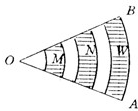
如图，把OA分成6个等分，以O为圆心画出六个扇形，已知最小的扇形面积是10平方厘米，则阴影部分的面积是

 

平方厘米．

Answer 1

分析：因为扇形的面积=

nπr2

360

，所以在圆心角一定时，扇形的面积与半径的平方成正比，把OA分成6个等分，以O为圆心画出六个扇形，所以扇形面积从小到大的比是1：4：9：16：25：36．由此求出阴影部分的面积．

解答：解：因为是六等份，
所以扇形面积从小到大的比是1：4：9：16：25：36．
所以扇形从小到大面积为10平方厘米，
10×4=40（平方厘米），
10×9=90（平方厘米），
10×16=160（平方厘米），
10×25=250（平方厘米），
10×36=360（平方厘米），
所以阴影部分的面积为（40-10）+（160-90）+（360-250）=210（平方厘米）
答：阴影部分的面积是210平方厘米．
故答案为：210．

点评：本题主要是利用扇形的面积公式得出在圆心角一定时，扇形的面积与半径的平方成正比，从而求出各个扇形的面积，进而求出阴影部分的面积．