题目内容
如图,将1至9九个数字写在一条纸带上,将它剪成三段,每段上数字连在一起算一个数,把这三个数相加,使和能被77整除,那么中间一段的数是
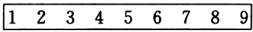
56
56
.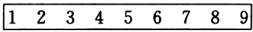
分析:由于1~9这九个数字相加的和是45,所以分成的三段之和是9的倍数.又由于和能被77整除,所以和能被77×9=693整除,所以只要考虑剪成三段后的三个数相加的和是否为693的倍数就可以解决了.
解答:解因为1~9这九个数字相加的和是45,所以分成的三段之和是9的倍数.
又由于和能被77整除,所以和能被77×9=693整除,
所以假设和为693,显然不合题意.
假设和为693×2=1386,由于123+456+789=1368,也不合题意.
假设和为693×3=2079,因为1234+56+789=2079,而2079÷77=27,
所以中间的一段数是56.
故答案为:56.
又由于和能被77整除,所以和能被77×9=693整除,
所以假设和为693,显然不合题意.
假设和为693×2=1386,由于123+456+789=1368,也不合题意.
假设和为693×3=2079,因为1234+56+789=2079,而2079÷77=27,
所以中间的一段数是56.
故答案为:56.
点评:此题主要考查了约数与倍数,利用已知得出和能被693整除是解题关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如下面左图,将1至9九个数依次排好,然后将上下两个数和左右两个数分别交换,重新排列后填入右图的方格内,使每一横行、竖列和两条对角线上各数的和都相等.算一算,这个和是
如下面左图,将1至9九个数依次排好,然后将上下两个数和左右两个数分别交换,重新排列后填入右图的方格内,使每一横行、竖列和两条对角线上各数的和都相等.算一算,这个和是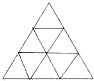 将1至9这九个自然数填人如图的九个小三角形中,使得由四个小三角形构成的三角形内的四个数之和都等于23.
将1至9这九个自然数填人如图的九个小三角形中,使得由四个小三角形构成的三角形内的四个数之和都等于23.