题目内容
15. 如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( )
如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( )| A. | P=Q | B. | P>Q | C. | P<Q | D. | 无法确定 |
分析 假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分阴影面积.
解答 解:扇形OAB的圆心角为90°,假设扇形半径为a,半圆半径为$\frac{1}{2}$a,
扇形面积:S=$\frac{90πa^2}{360}$=$\frac{πa^2}{4}$,
半圆面积为:M+Q=$\frac{1}{2}$π×($\frac{a}{2}$)2=$\frac{πa^2}{8}$,
又M+P=S-(M+Q)=$\frac{πa^2}{8}$=M+Q.
所以P=Q.
故选:A.
点评 此题主要考查了扇形面积求法,根据已知得出半圆面积以及扇形面积是解题关键.

练习册系列答案
相关题目
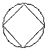 有一条对称轴.×.(判断对错)
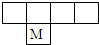
有一条对称轴.×.(判断对错) 如图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是( )
如图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是( )