题目内容
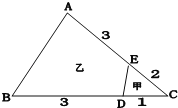
【题目】如图中的三角形被分成了甲、乙两部分，甲、乙两部分的面积之比是多少？（单位：厘米）
【答案】9：1
【解析】
试题分析：边接BE，△BDE与△DCE的高相同，面积的比就是底的比为3：1，△ABE与△BCE的高相同，它们面积的比就是底的比既3：2，设△DCE的面积是x，则△BDE的面积是3x，则△BCE的面积是4x，据此可求出△ABE的面积为多少．据此解答．
解：
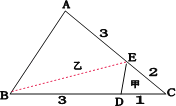
连接BE，根据分析知：
△BDE与△DCE的面积的比为3：1，
△ABE与△BCE面积的比为3：2，
设△DCE的面积为x，△BDE的面积就是3x，则△BCE的面积是：
3x+4x=4x，
△ABE的面积是：
4x×
=6x，
S甲：S乙=（S△ABE+S△BDE）：S△DCE=（6x+3x）：x=9x：x=9：1．
答：甲、乙两部分的面积之比是9：1．
练习册系列答案
智能训练练测考系列答案
相关题目
【题目】根据统计表完成练习。
一（3）班成绩统计表
考试成绩 | 100分 | 90－99分 | 80－89分 | 70－79分 | 60－69分 | 不及格 |
人数 | 6 | 16 | 7 | 4 | 1 | —— |
（1）成绩在（ ）分之间的人数最多，在（ ）分之间的人数最少。
（2）成绩在80－89分之间的人数比成绩在70－79分之间的人数（ ）（填“多”或“少”），比（ ）分之间的人数少，少（ ）人。
（3）一（3）班有2人缺考。你知道他们班现有多少人吗？