题目内容
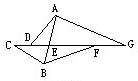
如图，已知CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是________．
40
分析：可以把S△ADE看成是一个整体，根据各线段的关系和左右两部分面积的关系，可以列出一个方程，求出S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．
解答：由题意知，S△AEG=3S△ADE，S△BFE=
S△BEC，
设S△ADE=X，则S△AEG=3X，S△BFE=（38-X），
可列出方程：（38-X）+3X=65，
解方程，得：x=10，
所以S△ADG=10×（1+3）=40．
故答案为：40．
点评：此题考查了如何利用边的关系求三角形的面积．
分析：可以把S△ADE看成是一个整体，根据各线段的关系和左右两部分面积的关系，可以列出一个方程，求出S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．
解答：由题意知，S△AEG=3S△ADE，S△BFE=
S△BEC，设S△ADE=X，则S△AEG=3X，S△BFE=
（38-X），可列出方程：
（38-X）+3X=65，解方程，得：x=10，
所以S△ADG=10×（1+3）=40．
故答案为：40．
点评：此题考查了如何利用边的关系求三角形的面积．
练习册系列答案
相关题目
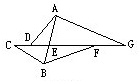
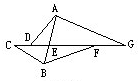
（2012?武汉模拟）如图，已知CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是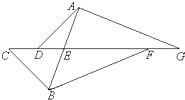
如图由三角形ADG和三角形BCF拼成，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65．已知CD=5，DE=7，EF=15，FG=6．那么三角形ADG面积是多少？
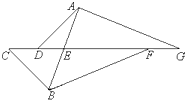如图由三角形ADG和三角形BCF拼成，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65．已知CD=5，DE=7，EF=15，FG=6．那么三角形ADG面积是多少？