题目内容
一个七位数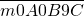 是33的倍数,我们计这样的七位数的个数为am.比如a5表示:形如
是33的倍数,我们计这样的七位数的个数为am.比如a5表示:形如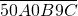 且是33的倍数的七位数的个数.则a2-a3=________.
且是33的倍数的七位数的个数.则a2-a3=________.
8
分析:一个七位数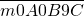 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,当m=2时,92+A+B+C是33的倍数,由于92+A+B+C≤92+27,即92+A+B+C≤119,所以92+A+B+C=99,则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,由插板法可知:共有
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,当m=2时,92+A+B+C是33的倍数,由于92+A+B+C≤92+27,即92+A+B+C≤119,所以92+A+B+C=99,则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,由插板法可知:共有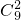 =36个符合要求的数,a2=36;当m=3时,93+A+B+C是33的倍数,由于93+A+B+C≤93+27,即93+A+B+C≤120,所以93+A+B+C=99,则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,由插板法可知:共有
=36个符合要求的数,a2=36;当m=3时,93+A+B+C是33的倍数,由于93+A+B+C≤93+27,即93+A+B+C≤120,所以93+A+B+C=99,则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,由插板法可知:共有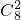 =28个符合要求的数,a3=28;据此可得a2-a3=36-28=8个.
=28个符合要求的数,a3=28;据此可得a2-a3=36-28=8个.
解答:一个七位数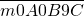 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,
当m=2时,92+A+B+C是33的倍数,
由于92+A+B+C≤92+27,
即92+A+B+C≤119,
所以92+A+B+C=99,
则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,
由插板法可知:共有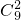 =36个符合要求的数,a2=36;
=36个符合要求的数,a2=36;
当m=3时,93+A+B+C是33的倍数,
由于93+A+B+C≤93+27,即93+A+B+C≤120,
所以93+A+B+C=99,
则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,
由插板法可知:共有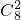 =28个符合要求的数,a3=28;
=28个符合要求的数,a3=28;
所以a2-a3=36-28=8个.
故答案为:8.
点评:解答此题关键是理解一个七位数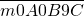 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,再分别求出当m=2时,和当m=3时,a2和a3的个数.
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,再分别求出当m=2时,和当m=3时,a2和a3的个数.
分析:一个七位数
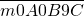 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,当m=2时,92+A+B+C是33的倍数,由于92+A+B+C≤92+27,即92+A+B+C≤119,所以92+A+B+C=99,则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,由插板法可知:共有
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,当m=2时,92+A+B+C是33的倍数,由于92+A+B+C≤92+27,即92+A+B+C≤119,所以92+A+B+C=99,则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,由插板法可知:共有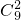 =36个符合要求的数,a2=36;当m=3时,93+A+B+C是33的倍数,由于93+A+B+C≤93+27,即93+A+B+C≤120,所以93+A+B+C=99,则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,由插板法可知:共有
=36个符合要求的数,a2=36;当m=3时,93+A+B+C是33的倍数,由于93+A+B+C≤93+27,即93+A+B+C≤120,所以93+A+B+C=99,则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,由插板法可知:共有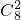 =28个符合要求的数,a3=28;据此可得a2-a3=36-28=8个.
=28个符合要求的数,a3=28;据此可得a2-a3=36-28=8个.解答:一个七位数
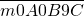 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,当m=2时,92+A+B+C是33的倍数,
由于92+A+B+C≤92+27,
即92+A+B+C≤119,
所以92+A+B+C=99,
则A+B+C=7,即(A+1)+(B+1)+(C+1)=10,
由插板法可知:共有
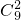 =36个符合要求的数,a2=36;
=36个符合要求的数,a2=36;当m=3时,93+A+B+C是33的倍数,
由于93+A+B+C≤93+27,即93+A+B+C≤120,
所以93+A+B+C=99,
则A+B+C=6,即(A+1)+(B+1)+(C+1)=9,
由插板法可知:共有
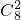 =28个符合要求的数,a3=28;
=28个符合要求的数,a3=28;所以a2-a3=36-28=8个.
故答案为:8.
点评:解答此题关键是理解一个七位数
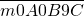 是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,再分别求出当m=2时,和当m=3时,a2和a3的个数.
是33的倍数,即m+A+B+9C=90+m+A+B+C是33的倍数,再分别求出当m=2时,和当m=3时,a2和a3的个数. 
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目