Question

（2011?东莞模拟）图中阴影部分的面积是

96

平方厘米．

Answer 1

分析：根据题干连接AC、BF，那么阴影部分的面积=正方形面积-△1的面积-△2的面积-△3的面积-△4的面积；抓住图形中的已知条件即可分析解决．

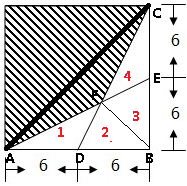
解答：解：根据图中数据，可以求得：△ABE=△CBD=（6+6）×6÷2=36平方厘米，且△1的面积=△4的面积；
因为D、E分别是的中点，不难得出△1=△2=△3=△4=36÷3=12平方厘米，
所以阴影部分的面积为：12×12-12×4=96（平方厘米），
故答案为：96．

点评：利用高一定时，三角形面积与底成正比的关系得出四个小三角形面积相等是解决此题的关键．