Question

1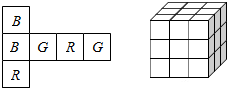． 如图所示的纸片可以沿虚线折成一个边长为1的正方体，这个正方体的六个面上各有一个字母R，G或B，制作27个这样的正方体，将他们以任意方式摆放成一个如图所示的边长为3的正方体，请问，在大正方体的表面积上最多能有几个字母R？答案：46．

Answer 1

分析 两个R是相连，一个正方体上最多只有2个面写字母R，制作27个这样的正方体，露在外面的面共有：3×3×6=54个，因为在顶点上三个面露在外面的正方体中，我们就要减去1个面，共有8个，用54减去8个即可，据此解答．

解答 解：3×3×6-8
=54-8
=46（个）；
答：在大正方体的表面积上最多能有46个字母R．
故答案为：46．

点评 本题要结合正方体的特征，要使含有字母R的面最多，就要尽量多的外漏，难点是确定顶点上的正方体最多有2个R的面外漏．