题目内容
1. 将1~13分别填入右图四个圆相互分割成的13个区域,然后把每个圆内的7个数相加,最后把四个圆的和再相加,总和最大是多少?最小是多少?
将1~13分别填入右图四个圆相互分割成的13个区域,然后把每个圆内的7个数相加,最后把四个圆的和再相加,总和最大是多少?最小是多少?
分析 经过观察发现,图中13个区域可以分成四种情况;第一种是四个圆的公共部分,第二种是三个圆的公共部分,第三种是二个圆的公共部分,第四种是一个圆单独的部分.由于题目要求总和最大,应满足圆与圆之间重叠次数较多的区域填尽可能大的数,如下图,区域a属于4个圆,应填13,b,c,d,e四个区域各属于3个圆,应填12,11,10,9,f,g,h,I四个区域,各属于2个圆,应填8,7,6,5,剩下四个区域只各属于1个圆,填最小的1,2,3,4,此时总和最大;
要想得到最小的值那么最大的几个数只能用的次数最少,所以只能填在最外面,只能用一次;重叠次数的越多的地方所填的数要越小,每个圆的和要接近.所以最大的四个数10、11、12、13填在四个圆的外面,6、7、8、9填在两个圆的相交处,2、3、4、5填在三个圆的相交处,1填在四个圆的相交处,这样就可以得到这个总和的最小值,据图计算即可.
解答 解:如下图,区域a属于4个圆,应填13,
b,c,d,e四个区域各属于3个圆,应填12,11,10,9,
f,g,h,I四个区域,各属于2个圆,应填8,7,6,5,
剩下四个区域只各属于1个圆,填最小的1,2,3,4,
此时总和最大,为:13×4+(12+11+10+9)×3+(8+7+6+5)×2+(4+3+2+1)=240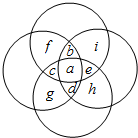
答:总和最大是240;
如图,根据分析把最大的数分别填在四个圆的外面,然后越往里面的数越小.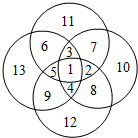
最小值为:10+11+12+13+(6+7+8+9)×2+(2+3+4+5)×3+1×4,
=46+60+42+4,
=152.
答:这个总和的最小可能值是152.
点评 此题考查了最大最小和图形的结合问题,把数字分成四部分,最大的数放在重叠次数多的地方,总和最大;大数用的次数最少入手,总和最小.

 名校课堂系列答案
名校课堂系列答案| A. | 大小相等,精确度不一样 | B. | 大小相等,精确度一样 | ||
| C. | 大小不等,精确度也不一样 |
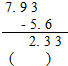 ×.(判断对错)
×.(判断对错)