题目内容
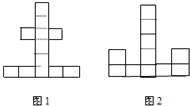
在如图所示的每个小方格中都填入一个整数:

并且任意三个相邻格子中所填数之和都等于5,则
=

并且任意三个相邻格子中所填数之和都等于5,则
| x+y+z |
| xyz |
-
| 1 |
| 108 |
-
.| 1 |
| 108 |
分析:断定与x相邻的两个数分别为9和2,求得x,然后依任意三个相邻格子中所填数之和都等于5,分别确定出每个格子中所填之数,可得到y、z,再将x、y、z代入
即可求出答案.
| x+y+z |
| xyz |
解答:解:容易断定与x相邻的两个数分别为9和2,
因为9+x+2=5,则x=-6,
依任意三个相邻格子中所填数之和都等于5,分别确定出每个格子中所填之数如下:9(-6)(2)9(-6)(2)(9)-6(2)(9)(-6)2(9)(-6)(2)(9)-6,
断定y=-6 z=9,
所以,
=
=-
.
故答案为:-
.
因为9+x+2=5,则x=-6,
依任意三个相邻格子中所填数之和都等于5,分别确定出每个格子中所填之数如下:9(-6)(2)9(-6)(2)(9)-6(2)(9)(-6)2(9)(-6)(2)(9)-6,
断定y=-6 z=9,
所以,
| x+y+z |
| xyz |
| -6-6+9 |
| (-6)×(-6)×9 |
| 1 |
| 108 |
故答案为:-
| 1 |
| 108 |
点评:此题主要考查数字有规律变化这个知识点,解答此题的关键是断定与x相邻的两个数分别为9和2,求得x.此题有一定的拔高难度,属于中档题.

练习册系列答案
相关题目

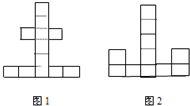 如图所示的每个小正方形的周长是4cm,那么“土”字的周长是
如图所示的每个小正方形的周长是4cm,那么“土”字的周长是