题目内容
五(一)班有50个学生选班长,有甲、乙、丙三个候选人,每人只能选他们之中的一个人,不能弃权.前40票中,甲得到20票,乙得到14票,丙得到6票,规定谁的票最多谁当选.若甲要一定当选,最少还需多少张票?
分析:从已知条件可知,50学生参选,已选40张,还剩下50-4080=10张选票.这10张选票全都选丙,丙得10+6=16张票,还比甲都少,所以丙不可能当选.我们再来分析甲和乙的选票.除去丙已得的6张票,甲和乙两人最多共可得44张票,为保证甲当选,则甲至少需要23票,还需要23-20=3张票.
解答:解:解:(50-6)÷2+1-20
=44÷2+1-20
=23-20
=3(张)
答:若甲要当选,最少还需要3张票.
=44÷2+1-20
=23-20
=3(张)
答:若甲要当选,最少还需要3张票.
点评:此题较难,解答此类题的关键是先求出未统计的票数,然后计算出甲和谁的票数相差最小,进而通过分析,得出甲要想当选,需要的票数,进而得出结论.

练习册系列答案
相关题目
 (2011?高县)五(1)班有40个学生,选一名同学任班长,选举结果如下表,下面( )图表示了这一选举结果.
(2011?高县)五(1)班有40个学生,选一名同学任班长,选举结果如下表,下面( )图表示了这一选举结果.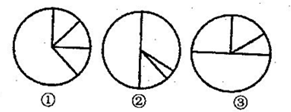 五(1)班有40个学生,选一名同学任班长,选举结果如下表,下面_____图表示了这一选举结果.
五(1)班有40个学生,选一名同学任班长,选举结果如下表,下面_____图表示了这一选举结果.