题目内容
算一算、填一填:
(1)小丽收集邮票240张,正好是小刚的 ,小兰和小刚收集的邮票张数的比是7:8.小兰收集邮票________张.
,小兰和小刚收集的邮票张数的比是7:8.小兰收集邮票________张.
(2)陈老师带一些钱去商店买练习本,刚好遇到促销,这种练习本打八折销售.这样,陈老师带去的钱刚好可以比原来多买100本练习本.已知每本练习本原来的售价是2.5元.陈老师一共带了________元钱.
(3)有一列数:3、6、8、8、4、2…从第三个数起,每个数都是它前面两个数乘积的个位数字,这一列数的2012个数是________.
解:(1)240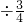 =320(张);
=320(张);
320×7÷8,
=2240÷8,
=280(张);
答:小兰收集邮票280张.
(2)2.5×80%×100,
=2×100,
=200(元);
200÷(1-80%),
=200÷20%,
=1000(元);
答:陈老师一共带了1000元.
(3)从第3个起为“6,8,8,4,2,8”循环;
(2012-2)÷6,
=2010÷6,
=335;
没有余数,那么第2012个数就是8.
故答案为:280,1000,8.
分析:(1)先把小刚的数量看成单位“1”,它的 对应的数量是240张,由此用除法求出小刚的数量;再根据小兰和小刚收集的邮票张数的比是7:8这一比例关系求出小兰的数量.
对应的数量是240张,由此用除法求出小刚的数量;再根据小兰和小刚收集的邮票张数的比是7:8这一比例关系求出小兰的数量.
(2)打八折是指现价是原价的80%,由此求出现价,100本的现价就是原来总钱数的1-80%,由此求出总钱数.
(3)这列数是:2,3,6,8,8,4,2,8,6,8,8,4,2,8,6,8,8,4,2,8…
可以看出从第3个起为“6,8,8,4,2,8”循环,因此第2012个数为:先减掉前2个不参加循环的2和3,然后再除以6,看余数是几,再根据余数判断.
点评:这类型的题目要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式计算.
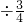 =320(张);
=320(张);320×7÷8,
=2240÷8,
=280(张);
答:小兰收集邮票280张.
(2)2.5×80%×100,
=2×100,
=200(元);
200÷(1-80%),
=200÷20%,
=1000(元);
答:陈老师一共带了1000元.
(3)从第3个起为“6,8,8,4,2,8”循环;
(2012-2)÷6,
=2010÷6,
=335;
没有余数,那么第2012个数就是8.
故答案为:280,1000,8.
分析:(1)先把小刚的数量看成单位“1”,它的
 对应的数量是240张,由此用除法求出小刚的数量;再根据小兰和小刚收集的邮票张数的比是7:8这一比例关系求出小兰的数量.
对应的数量是240张,由此用除法求出小刚的数量;再根据小兰和小刚收集的邮票张数的比是7:8这一比例关系求出小兰的数量.(2)打八折是指现价是原价的80%,由此求出现价,100本的现价就是原来总钱数的1-80%,由此求出总钱数.
(3)这列数是:2,3,6,8,8,4,2,8,6,8,8,4,2,8,6,8,8,4,2,8…
可以看出从第3个起为“6,8,8,4,2,8”循环,因此第2012个数为:先减掉前2个不参加循环的2和3,然后再除以6,看余数是几,再根据余数判断.
点评:这类型的题目要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,量一量,算一算,填一填.
如图,量一量,算一算,填一填.

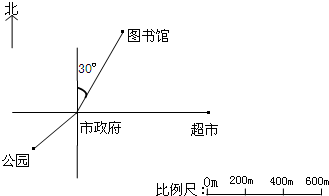
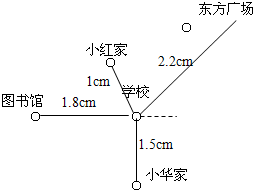 量一量,算一算,填一填.
量一量,算一算,填一填.